KNN算法

KNN算法
一、源码
from operator import attrgetter |
二、算法原理
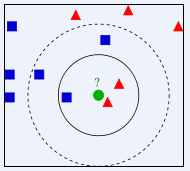
如上图所示,图中的数据可以分为蓝色正方形和红色三角形两类,图中心的绿色圆点是待分类数据,下面我们通过K最近领法对绿色圆点进行分类:
1.当k = 3 k=3k=3时,由图中实线圆内的数据可知:绿色圆点最近领的三个邻居中,一共有一个蓝色正方形和两个红色三角形,那么就可以将绿色圆点和红色三角形判定为一类。
2.当k = 5 k=5k=5时,由图中虚线圆内的数据可知:绿色圆点最近领的五个邻居中,一共有三个蓝色正方形和两个红色三角形,那么就可以将绿色圆点和蓝色正方形判定为一类。
至此,我们对KNN算法已经有了大概的了解。
三、算法步骤
1.初始化数据集
初始化训练集和测试集。训练集一般为两类或者多种类别的数据;测试集一般为一个数据。
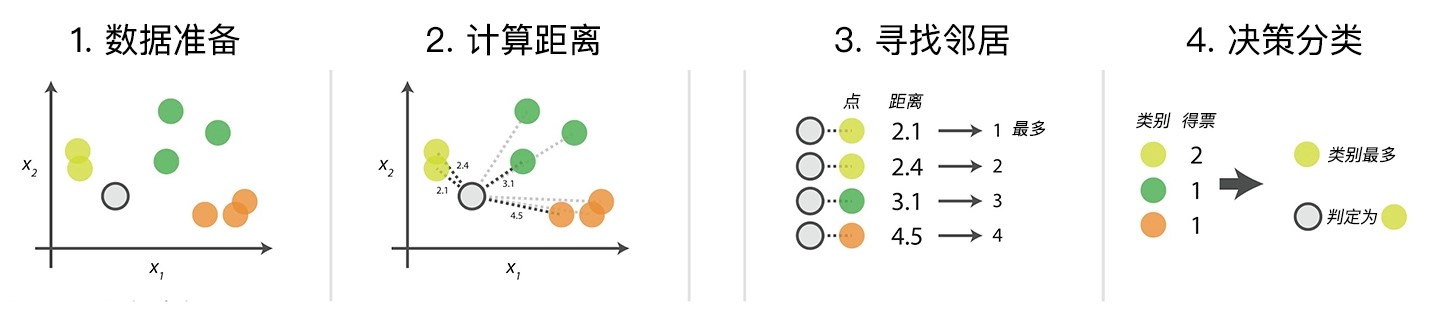
2.计算距离
计算测试数据到其他所有数据的距离,并记录下来。
常用到的距离计算公式如下:
①欧几里得距离(欧氏距离)
②曼哈顿距离
③闵可夫斯基距离
④切比雪夫距离
⑤马氏距离
⑥余弦相似度
⑦皮尔逊相关系数
⑧汉明距离
⑨杰卡德相似系数
⑩编辑距离
⑪DTW 距离
⑫KL 散度
3.寻找最近邻数据
将所有距离进行升序排序,确定K值,最近的K个邻居即距离最短的K个数据。
关于K值得选择问题:
- K 值的选择会对算法的结果产生重大影响。
- K值较小意味着只有与测试数据较近的训练实例才会对预测结果起作用,容易发生过拟合。
- 如果 K 值较大,优点是可以减少学习的估计误差,但缺点是学习的近似误差增大,这时与测试数据较远的训练实例也会对预测起作用,使预测发生错误。
- 在实际应用中,K 值一般选择一个较小的数值,通常采用交叉验证的方法来选择最优的 K 值。随着训练实例数目趋向于无穷和 K=1 时,误差率不会超过贝叶斯误差率的2倍,如果K也趋向于无穷,则误差率趋向于贝叶斯误差率。(贝叶斯误差可以理解为最小误差)
三种交叉验证方法:
Hold-Out: 随机从最初的样本中选出部分,形成交叉验证数据,而剩余的就当做训练数据。 一般来说,少于原本样本三分之一的数据被选做验证数据。常识来说,Holdout 验证并非一种交叉验证,因为数据并没有交叉使用。
K-foldcross-validation:K折交叉验证,初始采样分割成K个子样本,一个单独的子样本被保留作为验证模型的数据,其他K-1个样本用来训练。交叉验证重复K次,每个子样本验证一次,平均K次的结果或者使用其它结合方式,最终得到一个单一估测。这个方法的优势在于,同时重复运用随机产生的子样本进行训练和验证,每次的结果验证一次,10折交叉验证是最常用的。
Leave-One-Out Cross Validation:正如名称所建议, 留一验证(LOOCV)意指只使用原本样本中的一项来当做验证资料, 而剩余的则留下来当做训练资料。 这个步骤一直持续到每个样本都被当做一次验证资料。 事实上,这等同于 K-fold 交叉验证是一样的,其中K为原本样本个数。
4.决策分类
明确K个邻居中所有数据类别的个数,将测试数据划分给个数最多的那一类。即由输入实例的 K 个最临近的训练实例中的多数类决定输入实例的类别。
最常用的两种决策规则:
- 多数表决法:多数表决法和我们日常生活中的投票表决是一样的,少数服从多数,是最常用的一种方法。
- 加权表决法:有些情况下会使用到加权表决法,比如投票的时候裁判投票的权重更大,而一般人的权重较小。所以在数据之间有权重的情况下,一般采用加权表决法。
图示说明(其中K=4):